Optimal
Computing Budget Allocation (OCBA)
for
Simulation-based Decision Making Under Uncertainty (Simulation Optimization)
-- Find
the best design alternative using minimum simulation time
View This OCBA Page in Different
Languages
*** View this page in German, courtesy of StudyCrumb
*** View this page in Chinese, courtesy of
Prof.
Q.S. Jia and Mr. Di Wu at Tsinghua University, Beijing, China.
*** View this page in Indonesian language, courtesy of Jordan Silaen.
*** View this page in Belarusian language, courtesy of StudyBounty.com.
*** View this page in Russian, courtesy of The Art of Science.
*** View this page in Ukrainian, courtesy of SciPosts.
*** View this page in Czech language, courtesy of Andrey Fomin.
*** View this page in Polish language, courtesy of Valeria Aleksandrova.
*** View this page in Romanian, courtesy of azoft.
*** Find some most updated information at the OCBA Wikipedia site.
We have a state-of-the-art approach to intelligently allocate computing budget for efficient simulation optimization. The goal is to find the best design using a minimum simulation time. Many of our co-authors and friends contribute to enrich this area.
Simulation is a popular tool for designing large, complex, stochastic systems, since closed-form analytical solutions generally do not exist for such problems. While the advance of new technology has dramatically increased computational power, efficiency is still a big concern when using simulation for large system design, in which case many alternative designs must be simulated. To make the matter worse, multiple simulation runs must be performed for each design in order to catch stochastic behaviors in systems. How to dramatically reduce total computation time is the key issue in this topic.
A key component of our methodologies is our new control-theoretic simulation technique called Optimal Computing Budget Allocation (OCBA). The OCBA approach can intelligently determine the most efficient simulation replication numbers or simulation lengths for all simulated alternatives. The goal is to obtain the highest simulation decision quality using a fixed computing budget, or to attain a desired simulation decision quality using a minimum computing budget. Numerical testing shows that our approach can obtain the same simulation quality with only one-tenth the simulation effort.
OCBA is also ideal for stochastic simulation optimization. A primary reason that simulation optimization is difficult is the stochastic nature of evaluating the objective function, which means that there is a basic tradeoff between devoting computational effort on searching the space for new candidate solutions (exploration) versus getting more accurate estimates of the objective function at currently promising solutions (exploitation). In other words, how much of a simulation budget should be allocated to additional replications at already visited points and how much to replications at newly generated search points is a major consideration in terms of computational efficiency. In procedure, OCBA sequentially determines which design alternatives need more simulation and how many additional replications are needed.
Intuitively, to ensure that the best alternative is correctly selected, a larger portion of the computing budget should be allocated to those alternatives that are critical in the process of identifying the best alternative. In other words, a larger number of simulations must be conducted with those critical alternatives in order to reduce these critical estimators' variances. Overall simulation efficiency is improved as less computational effort is spent on simulating non-critical alternatives and more is spent on critical alternatives. The ideas are explained using the following simple example. Suppose we are performing simulations for 5 alternatives in order to determine an alternative with minimum mean delay. First of all, we conduct some preliminary simulation for all 5 alternatives. Figure 1-(a) gives an example of their 99% confidence intervals obtained from the preliminary simulation. Note that the uncertainty of estimation is due to the system's stochastic features and the use of Monte Carlo simulation.
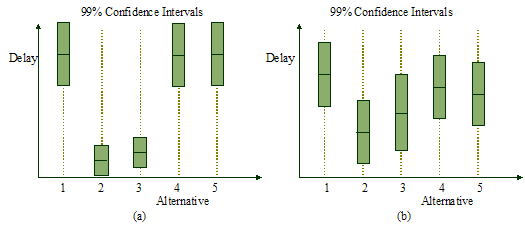
Figure
1. 99% confidence intervals
for five alternatives after some preliminary simulation in a (a) trivial case,
and (b) more common case.
As seen in Figure 1-(a), while there is uncertainty in the estimation of the performance for each alternative, it is obvious that alternatives 2 and 3 are much better than the other alternatives, if we intend to find an alternative with minimum mean delay. And so only alternatives 2 and 3 need to be further simulated to reduce estimation uncertainty in order to correctly identify the best alternative. By stopping simulations for alternatives 1, 4, and 5 earlier, we can save a lot of computation cost.
However, what actually happens in most cases is not as trivial as that shown in Figure 1-(a). It is more common to see cases like another example shown in Figure 1-(b), where some alternatives seem better, but are not clearly better than the others. It is not straightforward in such cases to determine which alternatives can be removed from the simulation experiment, and when they should be stopped. OCBA provides a systematic approach to address this problem and allocate simulation runs to alternatives in a way that the simulation efficiency is maximized.
To learn more about OCBA, the following two papers is a good starting point:
Introduction
of OCBA Ideas
Chen, C. H. and L. H. Lee, Stochastic Simulation Optimization: An Optimal Computing Budget Allocation. World Scientific Publishing Co., 2011.
Xu, J., E. Huang, L. Hsieh, L. H. Lee, Q. S. Jia, and C. H. Chen, "Simulation optimization in the era of Industrial 4.0 and the Industrial Internet," 10(4), 310-320, Journal of Simulation, 2016.
Xu, J., E. Huang, C. H. Chen, and L. H. Lee, "Simulation Optimization: A Review and Exploration in The New Era of Cloud Computing and Big Data," Asia-Pacific Journal of Operational Research, 32 (3), June 2015
Chen, C. H., M. Fu, and L. Shi, "Simulation and Optimization," Tutorials in Operations Research, pp. 247-260, Informs, Hanover, MD, 2008.
Fu, M, C. H. Chen, and L. Shi, "Some Topics for Simulation Optimization," Proceedings of 2008 Winter Simulation Conference, pp. 27-38, Miami, FL, December 2008.
Here are some more representative publications about the OCBA techniques.
One of Most Popular OCBA Papers
Chen, C. H., J. Lin, E. Yucesan, and S. E. Chick, "Simulation Budget Allocation for Further Enhancing the Efficiency of Ordinal Optimization," Journal of Discrete Event Dynamic Systems: Theory and Applications, Vol. 10, pp. 251-270, July 2000.
Earlier Development of OCBA
Chen, C. H. "An Effective Approach to Smartly Allocate Computing Budget for Discrete Event Simulation," Proceedings of the 34th IEEE Conference on Decision and Control, pp. 2598-2605, December 1995.
Chen, C. H. "A Lower Bound for the Correct Subset-Selection Probability and Its Application to Discrete Event System Simulations," IEEE Transactions on Automatic Control, Vol. 41, No. 8, pp. 1227-1231, August 1996.
Chen, C. H., E. Yucesan, L. Dai, and H. C. Chen, "Efficient Computation of Optimal Budget Allocation for Discrete Event Simulation Experiment," IIE Transactions, Vol. 42, No. 1, pp. 60-70, January 2010.
OCBA for Problems with Multiple
Objectives
Lee, L. H., E. P. Chew, S. Y. Teng, and D. Goldsman, "Optimal computing budget allocation for multi-objective simulation models," Proceedings of 2004 Winter Simulation Conference, pp. 586-594, 2004.
E.J. Chen and L.H. Lee, "A multi-objective selection procedure of determining a Pareto set", Computers and Operations Research, 36(6), : 1872-1879 , 2009.
S. Teng, L.H. Lee and E.P. Chew, "Integration of Indifference-zone with Multi-objective Computing Budget Allocation", European Journal of Operational Research, 203(2): 419-429, 2010.
L. H. Lee, E. P. Chew, S. Y. Teng, and D. Goldsman (2010). Finding the Pareto set for multi-objective simulation models, to appear in IIE Transactions.
OCBA for Selecting An
Optimal Subset of Top Designs (say top 5)
Chen, C. H., D. He, M. Fu, and L. H. Lee, "Efficient Simulation Budget Allocation for Selecting an Optimal Subset," Informs Journal on Computing, Vol. 20, No. 4, pp. 579-595, 2008.
Zhang, S., L. H. Lee, E. P. Chew, J. Xu, and C. H. Chen, "A Simulation Budget Allocation Procedure for Enhancing the Efficiency of Optimal Subset Selection," IEEE Transactions on Automatic Control, 61(1), 62-75, January 2016.
OCBA for Selecting the Best
Alternative when Samples Are Correlated
Fu, M. C., J. Q. Hu, C. H. Chen, and X. Xiong, "Simulation Allocation for Determining the Best Design in the Presence of Correlated Sampling," Informs Journal on Computing, Vol. 19, No. 1, pp. 101-111, 2007.
OCBA for Simulation and Optimization
Zhang, S., J. Xu, L. H. Lee, E. P. Chew, W. P. Wong, and C. H. Chen, "Optimal Computing Budget Allocation for Particle Swarm Optimization in Stochastic Optimization," IEEE Transactions on Evolutionary Computation, 21(2), 206-219, 2017.
Nicholas, P., "A Dividing Rectangles Algorithm for Stochastic Simulation Optimization," Proceedings of 14th INFORMS Computing Society Conference, Richmond, Virginia, January 2015.
He, D., L. H. Lee, C. H. Chen, M. Fu, and S. Wasserkrug, "Simulation Optimization Using the Cross-Entropy Method with Optimal Computing Budget Allocation," ACM Transactions on Modeling and Computer Simulation, 2009.
Chew, E. P. , L.H. Lee, S.Y. Teng, and C.H. Koh, "Differentiated Service Inventory Optimization using Nested Partitions and MOCBA", Computers and Operations Research, 36(5), : 1703-1710, 2009.
Lee, L. H., E.P. Chew, S.Y. Teng, and Y.K. Chen, "Multi-objective simulation-based evolutionary algorithm for an aircraft spare parts allocation problem", European Journal of Operational Research, 189 (2): 476-491, 2008.
Chen, C. H., D. He, M. Fu, and L. H. Lee, "Efficient Simulation Budget Allocation for Selecting an Optimal Subset," Informs Journal on Computing, Vol. 20, No. 4, pp. 579-595, 2008.
Shi, L. and C. H. Chen, "A New Algorithm for Stochastic Discrete Resource Allocation Optimization," Journal of Discrete Event Dynamic Systems: Theory and Applications, Vol. 10, pp. 271-294, July 2000.
Applications of OCBA
Hsieh, L., E. Huang, and C. H. Chen, "Equipment Utilization Enhancement in Photolithography Area through a Dynamic System Control Using Multi-fidelity Simulation Optimization with Big Data Technique," IEEE Transactions on Semiconductor Manufacturing Decision, 30(2), 166-175, 2017.
Aristotelis, T., M. Bastani, N. Celik, and C. H. Chen,
"Dynamic Data Driven Adaptive Simulation Framework for Automated Control
in Microgrids," IEEE Transactions on
Smart Grid, 8(1), 209-218, 2017.
Hsieh, L., E. Huang, S. Zhang, K. H. Chang, C. H. Chen, "Application of Multi-Fidelity Simulation Modeling to Integrated Circuit Packaging," International Journal of Simulation and Process Modelling, 28(2), 195-208, Spring 2016.
Hsieh, B. W., C. H. Chen, S. C. Chang, "Efficient Simulation-based Composition of Dispatching Policies by Integrating Ordinal Optimization with Design of Experiment," IEEE Transactions on Automation Science and Engineering, Vol. 4, No. 4, pp. 553-568, October 2007.
Romero, V. J., D. V. Ayon, C. H. Chen, "Demonstration of Probabilistic Ordinal Optimization Concepts to Continuous-Variable Optimization Under Uncertainty," Optimization and Engineering, Vol. 7, No. 3, pp. 343-365, September 2006.
Chen, C. H., and D. He, "Intelligent Simulation for Alternatives Comparison and Application to Air Traffic Management," Journal of Systems Science and Systems Engineering, Vol. 14, No. 1, pp. 37-51, March 2005.
Chen, C. H., K. Donohue, E. Yucesan, and J. Lin, "Optimal Computing Budget Allocation for Monte Carlo Simulation with Application to Product Design," Journal of Simulation Practice and Theory, Vol. 11, No. 1, pp. 57-74, March 2003.
Hsieh, B. W., C. H. Chen, and S. C. Chang,
"Scheduling Semiconductor Wafer Fabrication by Using Ordinal
Optimization-Based Simulation," IEEE
Transactions on Robotics and Automation, Vol. 17, No. 5, pp. 599-608, October 2001.
Chen, C. H., S. D. Wu, and L. Dai, "Ordinal
Comparison of Heuristic Algorithms Using Stochastic Optimization," IEEE Transactions on Robotics and Automation,
Vol. 15, No. 1, pp. 44-56, February 1999.
Association with Ordinal Optimization
Dai, L., C. H. Chen, and J. R. Birge, "Large Convergence Properties of Two-Stage Stochastic Programming," Journal of Optimization Theory and Applications, Vol. 106, No. 3, pp. 489-510, September 2000.
Ho, Y. C., C. G. Cassandras, C. H. Chen, and L. Dai, "Ordinal Optimization and Simulation," Journal of Operational Research Society, Vol. 51, No. 4, pp. 490-500, April 2000.
Dai, L. and C. H. Chen, "Rate of Convergence for Ordinal Comparison of Dependent Simulations in Discrete Event Dynamic Systems," Journal of Optimization Theory and Applications, Vol. 94, No. 1, pp. 29-54, July 1997.
Some Other Generalizations and
Related Works
Blanchet, J., J. Liu, and B. Zwart, "Large Deviations Perspective on Ordinal Optimization of Heavy-Tailed Systems," Proceedings of the 2007 Winter Simulation Conference, pp. 489-494, 2007.
Branke, J., S. E. Chick, and C. Schmidt. Selecting a selection procedure. Management Science 53 1916-1932, 2007.
Chick, S. and K. Inoue. New two-stage and sequential procedures for selecting the best simulated system. Operations Research 49 1609-1624, 2001.
Chick, S. and K. Inoue. New procedures to select the best simulated system using common random numbers. Management Science 47 1133-1149, 2001.
Glynn, P., S. Juneja. A Large deviations perspective on ordinal optimization. Proceedings of the 2004 Winter Simulation Conference, 577-585, 2004.
Pujowidianto, N. A., L. H. Lee, C. H. Chen, C. M. Yep, "Optimal Computing Budget Allocation For Constrained Optimization," to appear in Proceedings of 2009 Winter Simulation Conference, pp. 584-589, Austin, TX, December 2009.
Trailovic, L. and L. Y. Pao. 2004. Computing budget allocation for efficient ranking and selection of variances with application to target tracking algorithms. IEEE Transactions on Automatic Control 49 58-67, 2004.
OCBA Books
1. A new book about OCBA has been published in 2011. The name of the book is "Stochastic Simulation Optimization: An Optimal Computing Budget Allocation". This book gives a comprehensive and extensive coverage on this efficient simulation optimization methodology, from basic idea, formal development, to the state-of-art. You can order it from Amazon.com.
2. Another new book extending to a much broader perspective of ordinal optimization is "Stochastic Simulation Optimization for Discrete Event Systems - Perturbation Analysis, Ordinal Optimization, and Beyond", published in 2013.
Computer
Source Codes for OCBA
- OCBA C Code, which also appears on pages 214 - 218 of the OCBA book.
- OCBA C++ Code, courtesy of Prof. Nurcin Celik at University of Miami
- OCBA JAVA Code, courtesy of Prof. Nurcin Celik at University of Miami
OCBA Demo
(and JAVA code)
OCBA Demo Using Your Web browser. This demo of OCBA is implemented by A. Johnson, Cheol Y. Park, and Ning Lin. In the demo, you will see how OCBA dynamically select the worthies designs for further simulation.
Go to Professor Chun-Hung Chen's Page
Go to Professor Loo Hay Lee's Page
Go to Professor Q. S. Jia's Page
Go to Professor Nurcin Celik's Page
